Home / Statistical Tools / Reliability / Uncensored / Reliability: Fitting Uncensored Data
Reliability: Fitting Uncensored Data¶
From Excel click...
QXL Stat Tools Tab > Reliability > Uncensored > Choose Distribution
Quantum XL can fit both Censored and Uncensored Data. This topic covers uncensored. If your data is censored, see Fitting Censored Data.
Quantum XL supports fitting the following distributions: 2-Parameter Normal, 1-Parameter Exponential, 2-Parameter Exponential, 2-Parameter Logistic, 2-Parameter LogLogistic, 3-Parameter LogLogistic, 2-Parameter LogNormal, 3-Parameter LogNormal, 2-Parameter Weibull, 3-Parameter Weibull, 2-Parameter Gumbel/Smallest Extreme Value (SEV), and Johnson Distribution.Auto-Fit will analyze your dataset, fit all of the available distributions, and then present the results in rank order.
Step #1: Select data source for Analysis.¶
The data should be in one column. For more information about data format, see Uncensored Data Format.
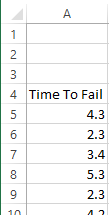
Step #2¶
From Excel click...
QXL Stat Tools Tab > Reliability > Uncensored > Choose Distribution
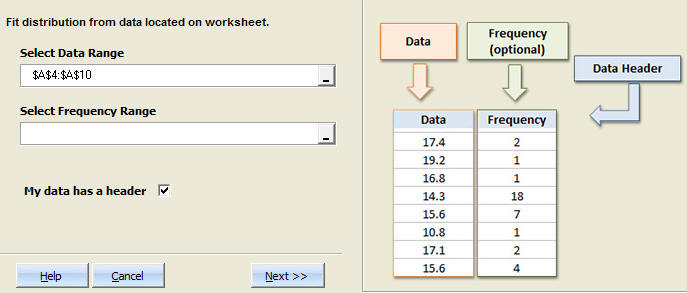
Step #3: Select the data range which contains your data.¶
Step 4: Enter Spec Limits and Confidence Interval¶
If you provide specification limits, Quantum XL will calculate the area out of specification. Change the confidence interval for the resulting analysis (optional). If you wish to have a hazard and survivor plot created, check the checkbox (optional). When you're done selecting the desired options, click on the "Create reports for selected distributions" button.
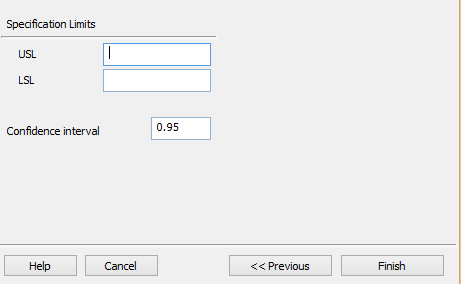
Specification Limits (Optional): If you enter the Upper and/or the Lower Specification Limit, Quantum XL will calculate the associated probabilities in the report.
Confidence Interval: The resulting report will include confidence intervals for estimated parameters. The default value is 95%, but you may enter any value greater than 0 and less than 1.
Step 5: Click "Finish". Quantum XL will create the analysis.¶
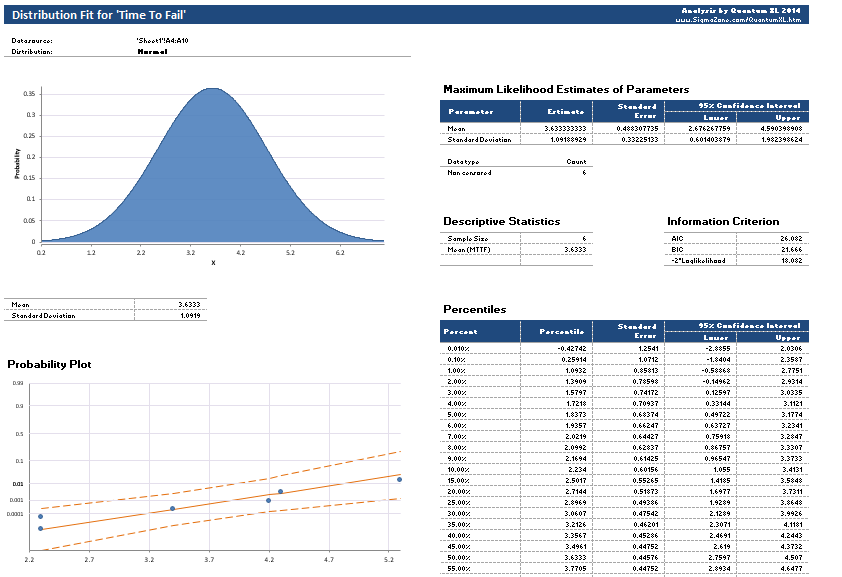
For more information about the analysis, see Understanding Distribution Fit Results.