Home / Statistical Tools / Distribution Fit/Calc / Distribution Calculator / Hypergeometric Distribution
Hypergeometric Distribution¶
Probability Calculator¶
From Excel click...
QXL Stat Tools Tab > Distribution Fit/Calc > Distribution Calculator >Hypergeometric
The Hypergeometric distribution is a discrete probability distribution. It can be used to calculate the probability of x successes in n draws without replacement from a finite population of size N containing K successes. If the population is infinite or the draws occur with replacement, then the Binomial distribution can be used.

Like the Binomial, Negative Binomial, and Geometric distributions, the Hypergeometric is based on Bernoulli Trials. However, it is unique in that it can calculate from a non-infinite population. With the other three distributions, the p is assumed constant during the trials. The Hypergeometric doesn't make this assumption. Instead it uses the Population Size (N) and Number Successes in the Population (K) to calculate the initial Probability of Success (p). However, once draws begin, the probability of success will change. For example, in a deck of cards, we can define a heart card as a success in the Initial Population Size (N) = 52 and the Number of Successes in the Population (K) = 13. After the first card is drawn, both the N and K will change which will change the probability of drawing a heart. The Hypergeometric distribution is uniquely able to handle the change in p over the course of the experiment.
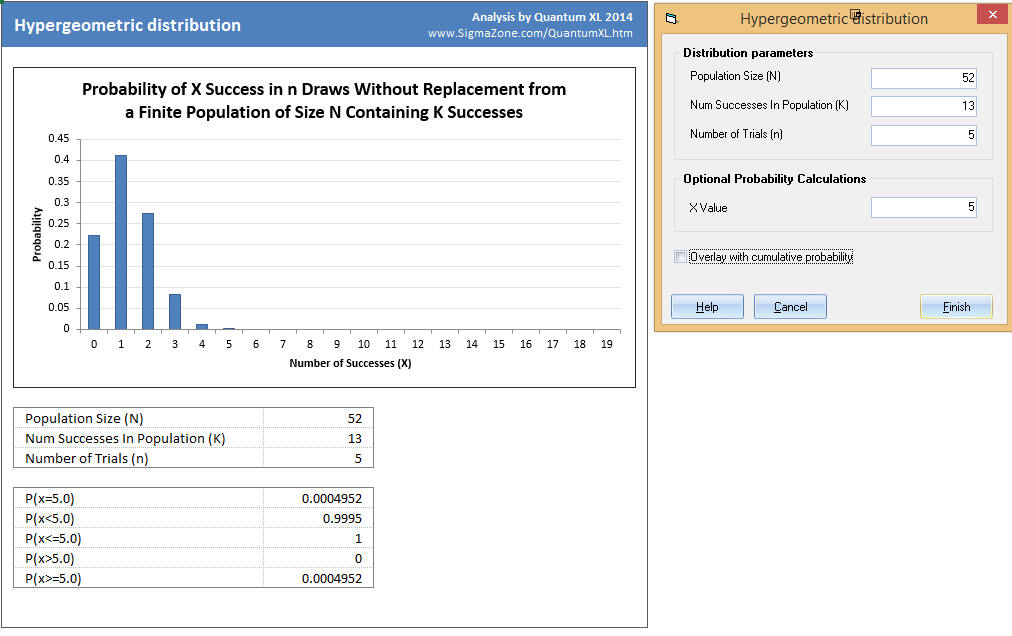
Example¶
A standard deck of playing cards (without Jokers) has 52 cards and four suits (diamonds, hearts, spades, and clubs). Suppose you wanted to know the probability of drawing 5 consecutive hearts.
Using the Hypergeometric distribution...
Population Size = 52 (the number of cards)
Number of Successes In Population = 13 (number of hearts in a deck)
Number of Trials = 5 (five consecutive hearts)
The results from Quantum XL are below. The blue bars indicate the probability of having (x) successes. For example, the probability of having zero successes (drawing no hearts in five cards) is just over 20%. The probability of drawing 1 heart is just over .4. The numerical values at the bottom of the analysis indicate that the probability of five hearts, or P(x=5), is .0004952, or roughly .05%.