Home / DOE / Additional Information / Understanding Least Square Residuals
Understanding Least Square Residuals¶
Residual analysis is a method of regression diagnostics. Residuals can help you identify influential points (potential outliers), lack of fit issues, and other patterns. The ultimate goal is to improve the model.
Residuals¶
Residuals, often denoted as ei, are the observed minus the predicted or Yi-Ŷ. One of the assumptions of regression is that the residuals should be Normally distributed with a mean of zero and a standard deviation equal to the standard error.
ei~N(0,σ2error)
Studentized Residual¶
Studentized residuals are normalized by dividing each residual by the standard error. This makes the standardized residuals N(0,12). Most experimenters will investigate any value outside the range -3 to +3 as outliers.
R-Studentized Residuals¶
R-Studentized residuals are similar to the studentized residuals except that the standard error is recalculated without the ith data point. Many experimenters will investigate any value outside the range +/- 3.5.
Leverage¶
The leverage is the relative impact of each point on the model. Points with higher leverage influence the coefficients more than low leverage points. High leverage points are not by themselves problematic. However, a combination of high leverage and an outlier can significantly reduce the predictive abilities of a model.
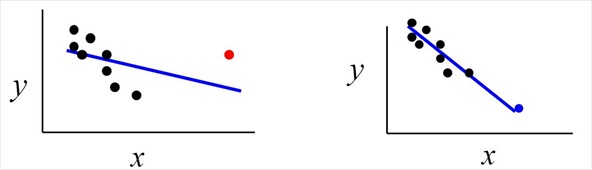
In the plot below, the red point on the left is both high leverage and an outlier. This point will "pull" the model away from the ideal fit. In the model on the right, the blue point is high leverage but not an outlier. This point will provide a better estimate for the model.
Cook's D¶
Cook's D or Cook's Distance is a combination of the standardized residual and the leverage to provide a single number which measures the impact of each data point. Values that are disproportionally larger have a greater impact on the model.
In his original text, Dennis Cook suggested that values greater than 1 indicated highly significant points (Cook and Stanford (1982). Residuals and influence in regression, Chapman & Hall). Bollen and Jackman suggest that values greater than 4/n where N is the number of observations indicate significant points (Bollen and Jackman (1980); Regression diagnostics: An expository treatment of outliers and influential cases, in Modern Methods of Data Analysis. Sage).
Note
- Influential points are not necessarily outliers. Additional investigation is advised before classifying an influential point as an outlier.
- Removal of influential points can significantly change regression coefficients as well as the regression statistics such as the R2, Standard Error, and F Value.