Home / DOE / Create Designs / Create Central Composite (CCD) Design

Create Central Composite (CCD) Design¶

From Excel click...

QXL DOE Tab > Create Design > Create Central Composite Design

Central Composite Designs can be created by selecting QXL DOE Tab > Create Design > Create Central Composite Design.

Select the base design¶

Central Composite Designs (CCD) are based on a Full or Fractional Factorial. You may select the desired base design by clicking on the grid of choices. The Number of Factors is in the columns, while the level of factorial is in rows. For example: if you have five factors you can choose between using the Full Factorial, the Half Factorial (Resolution V) and the Quarter Factorial (Resolution IV).

CCD

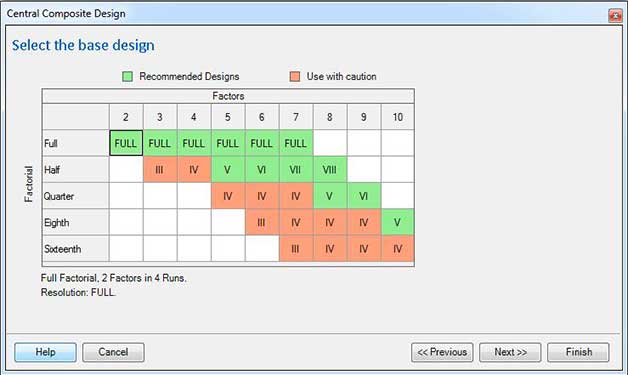
Any design that is Resolution V or higher is green while Resolution IV and lower are red. Most experimenters would prefer to have the base design at Resolution V or higher.

Enter Factor Names and Coding¶

The Central Composite Design is not compatible with Categorical (qualitative) variables. Therefore, when entering the factor names and coding, all inputs are assumed to be Quantitative.

Factor name: Enter a unique name for the factor. Make the name short but descriptive. For example, use "Temp" instead of "Temperature" as it will make reading the results in the regression table easier.

Levels: Enter the Low and High values for each variable. For example, if you would like to experiment with temperature from 100 to 200 degrees, replace -1 with 100 and +1 with 200.

Define Outputs (responses)¶

Click here for more information...

Axial and center points¶

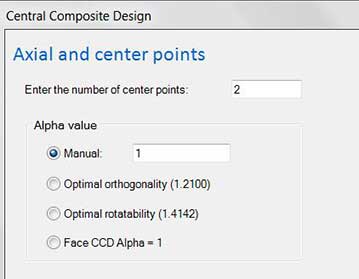
CCD Alpha

Enter the number of center points: Type in the number of center points you would like in your experiment.

Alpha value¶

Choose between…

Manual
Optimal orthogonality
Rotatable
Spherical
Face CCD

Note

Quantum XL calculates the optimal alpha for orthogonality and rotatability. It is dependent on the design (number of factors) and the number of center points.

Orthogonal: Alpha is set to the value that minimizes the Variance Inflation Factors. For most designs, it is possible to obtain VIFs = 1 for all factors, although the required value for alpha may be too large to be practical.

Rotatable: Alpha is chosen so that each of the points has the same magnitude of prediction error. Note that in most rotatable designs, the factorial and axial points lie in different concentric geometric spheres. If you would like all points on the same concentric sphere, use the spherical design.

Spherical: All design points occur on the same geometric sphere. These designs are "nearly" rotatable.

Face Centered: Defined as alpha = 1. The axial values are located on the surface of the square, cube, or hypercube.

Note

Practically, there is very little difference between a rotatable and spherical design. The alpha values will be very close (or equivalent) for most designs.