Home / DOE / Analyze / Binary Logistic Regression
Binary Logistic Regression¶
Binary Logistic Regression is used by Quantum XL during Run Regression when the output is binary. Binary outputs have two possible values. They can be 0/1, True/False, Male/Female, etc. If the output is categorical but has more than two levels, use Nominal Logistic Regression.
Binary logistic regression is actually a misnomer. Unlike Ordinary Least Squares Regression (OLS) the coefficients are an estimate of an iterative algorithm called Newton's Method.
While OLS has often been used to model binary data, it suffers from the problem that values greater than 1 (100% probability) and 0 (0% probability) can be predicted by the resulting model. Binary logistic regression uses the Logistic Function to ensure this can never happen. The most common forms of the Logistic function are in the diagram below.
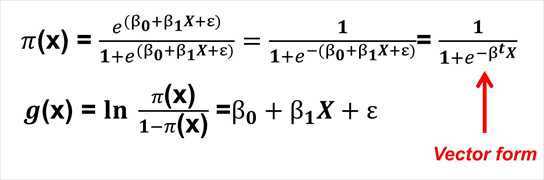
Where π is the predicted proportion, β are the regression coefficients, and x a covariate pattern (or row from the X matrix).
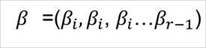
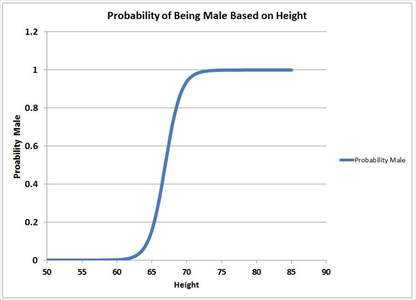
Example: Using the logistic function, the diagram below was created. Note that values less than 0 or greater than 1 do not occur.
Values for β (regression coefficients) are estimated using Newton's algorithm which maximizes the log of the maximum likelihood function (see L below).
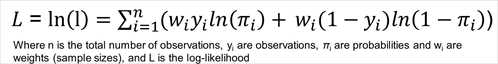
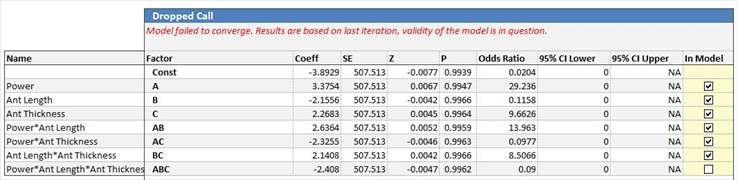
Newton's Algorithm, also known as Newton's iterations, are not guaranteed to converge. Quantum XL will warn you that a model failed to converge by displaying a warning in red at the top of the regression table.